2025年5月16日 写真を追加しました。
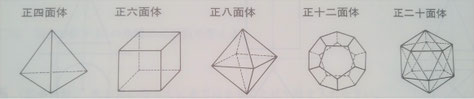
正多面体はイメージしにくい?
【正多面体】というものがあります。

【正四面体】・【正六面体】・【正八面体】・【正十二面体】・【正二十面体】と五種類ある、数学や受験算数でお馴染みの立体です。
問題は、この【正多面体】の教え方というか、導入です。
なんというか、うまく表現しにくいのですが、【正多面体】になると、
全体的に生徒の反応が弱くなっちゃう
というか、
薄くなっちゃう
というか、
スムーズにいかなくなっちゃう
感じなんですね。
他塾の方に聞いても似たような感じだそうでして、テキストに【正多面体】の図が載ってはいるものの、二次元の平面図ということもあり、生徒にとっては立体としてイメージしにくいのかもしれません。
特に【正四面体】【正八面体】【正二十面体】は「正三角形」でできているのに、【正十二面体】は「正五角形」で構成されているということが、ピンとこないようです。
また、過去に【正四面体】をピラミッド形と思い込む生徒もいました😢
結局、イメージしにくいので「頂点の数・辺の数」を計算で導くのが困難になってしまい、丸暗記しようとする生徒も出てきてしまいます😢
いやいや、流石に丸暗記は無理でしょ
と思うのですが、世の中には
語呂合わせで丸暗記しちゃおう
という方針の塾もあるそうでして・・
語呂合わせ派の塾さんを敵に回すつもりはないのですが、「頂点の数・辺の数」はやっぱり計算で出してほしい。
ただ、計算するには【正多面体】をきちんと立体としてイメージできる必要がある・・
なんか、こう、堂々巡りでした。
もちろん、模型を使うことも考えました。
立体については理屈ではなく、実物を手に取ってみるのが一番ですからね。
実際に触れてみればイメージがつかめます。
ただ、市販されている模型は耐久性に難がありまして、そして業務用の本格的な模型はなかなかに高価でして、これを全五種類、対象生徒全員に配布する(進呈する)というのはちょっと難しい・・
セリアに正多面体が!
そんな中、他塾の方から
100均に正多面体が売っている!
と教えてもらいました!

正多面体 全五種類が入って税込110円!
一個110円ではなく、全五種類が入って110円です。
費用的には大変ありがたいのですけど、これって、100均ショップとして採算に合うのでしょうか?

ちなみにダイソーさんではなくセリアさんです。(セリアさんの大型店でよく見かけます。小型店にはあまり置いてない印象です)
【正四面体】【正八面体】【正二十面体】

これなら実際に生徒に配布する(進呈する)事ができます。余裕でできます(笑)
そして実物に触れることができれば、こっちのものです(笑)
生徒に【正多面体】全五種類を渡し、まずは「正三角形」シリーズの【正四面体】【正八面体】【正二十面体】を目の前に並べてもらいます。
その際、事前に「正三角形」の一つの内角は60°という、当たり前のことを確認しておきます。
で、とんがったところ(頂点)が真上に来るようにして【正四面体】【正八面体】【正二十面体】を上からのぞき込んでもらいます。
すると【正四面体】は「正三角形」三枚が集合して頂点が構成されていることがわかります。
同様に【正八面体】は「正三角形」四枚が集合して頂点が構成されていて、そして【正二十面体】は「正三角形」五枚が集合して頂点ができていることがわかります。
ちなみに「正三角形」の集合が六枚になると「正三角形」の一つの内角は60°ですので、60°×6=360°と平面になってしまい、とんがったところ(頂点)は作ることが出来ないなんてことも、あっさりとわかってもらえます。
こうやって文字に書くとわかりにくいのですが(笑)、実際には実物を手に取ってもらいながらの説明ですので、結構スムーズに理解してもらえます。
【正六面体】
「正三角形」の次は「正四角形」シリーズの【正六面体】です。
僕は【正多面体】の時は、なるべく正方形と言わずに「正四角形」、立方体と言わずに【正六面体】と言うように意識しているのですが、どうやら生徒にとってはどっちでもいいみたいです(笑)
もちろん「正四角形」の一つの内角は90°という、超当たり前のことを確認しておきます。
で、とんがったところ(頂点)が真上に来るようにして【正六面体】を上からのぞき込んでもらい、「正四角形」三枚が集合して頂点が構成されている事を確認してもらいます。
ちなみに「正四角形」の集合が四枚になると、90°×4=360°と平面になってしまい、頂点は作成不可能なことも、理解してもらえます。
【正十二面体】

最後に「正五角形」シリーズの【正十二面体】です。
ここであらかじめ「正五角形」の一つの内角は180°×3÷5=108°を確認しておきます。
そして頂点が真上に来るようにして【正十二面体】を上からのぞき込んでもらい、「正五角形」三枚が集合して頂点が構成されている事を確認してもらいます。
ちなみに「正五角形」の集合が四枚になると、108°×4=432°と360°を超えてしまい、頂点は作成不可能なことも、あっさりとわかってもらえます。
なお、「正三角形」➡「正四角形」➡「正五角形」ときたので、次は「正六角形」だ!と行きたいところですが・・
「正六角形」の一つの内角は120°ですので、「正六角形」が三枚集合するだけで120°×3=360°と平面になってしまい、頂点を作れません。
同様に「正七角形」「正八角形」「正九角形」・・も頂点を作れません。
頂点の数・辺の数
【正多面体】をきちんと立体としてイメージできるようになったら「頂点の数・辺の数」が計算で出せるはずです。
【正十二面体】を例にして考えてみます。
頂点の数
面の形は「正五角形」ですから、一つの面に頂点は5個。
そしてその「正五角形」が12面あるのですから、本来、頂点の数は5×12=60個となるはずです。
しかし実際には、三つの頂点が重複して一つの頂点になっているので、60÷3=20個となります。
辺の数
やはり「正五角形」ですから、一つの面に辺は5本。
そしてその「正五角形」が12面あるのですから、本来、辺の数は5×12=60本となるはずです。
しかし実際には、各面が立体として組み合わさるときに、二本の辺が重なって一本の辺になっているので、60÷2=30本となります。
次に【正二十面体】を例にして考えてみます。
頂点の数
面の形は「正三角形」ですから、一つの面に頂点は3個。
そしてその「正三角形」が20面あるのですから、本来、頂点の数は3×20=60個となるはずです。
しかし実際には、五つの頂点が重複して一つの頂点になっているので、60÷5=12個となります。
辺の数
やはり「正三角形」ですから、一つの面に辺は3本。
そしてその「正三角形」が20面あるのですから、本来、辺の数は3×20=60本となるはずです。
しかし実際には、各面が立体として組み合わさるときに、二本の辺が重なって一本の辺になっているので、60÷2=30本となります。
同様に他の【正多面体】の「頂点の数・辺の数」を計算すると、以下の表のようになります。
|
面 |
頂点 | 辺 | |
| 【正四面体】 | 4面 | 4 |
6 |
| 【正六面体】 | 6面 | 8 |
12 |
| 【正八面体】 | 8面 | 6 |
12 |
| 【正十二面体】 |
12面 |
20 |
30 |
| 【正二十面体】 |
20面 |
12 | 30 |
なお【正六面体】と【正八面体】は、面の数と頂点の数が入れ替わる関係です。
|
面 |
頂点 | 辺 | |
| 【正四面体】 | 4面 | 4 |
6 |
| 【正六面体】 | 6面 | 8 |
12 |
| 【正八面体】 | 8面 | 6 |
12 |
| 【正十二面体】 |
12面 |
20 |
30 |
| 【正二十面体】 |
20面 |
12 | 30 |
同様に【正十二面体】と【正二十面体】も面の数と頂点の数が入れ替わっています。
|
面 |
頂点 | 辺 | |
| 【正四面体】 | 4面 | 4 |
6 |
| 【正六面体】 | 6面 | 8 |
12 |
| 【正八面体】 | 8面 | 6 |
12 |
| 【正十二面体】 |
12面 |
20 |
30 |
| 【正二十面体】 |
20面 |
12 | 30 |
ちなみに【正四面体】は、自分自身と(?)面の数と頂点の数が入れ替わる関係です。
|
面 |
頂点 | 辺 | |
| 【正四面体】 | 4面 | 4 |
6 |
| 【正六面体】 | 6面 | 8 |
12 |
| 【正八面体】 | 8面 | 6 |
12 |
| 【正十二面体】 |
12面 |
20 |
30 |
| 【正二十面体】 |
20面 |
12 | 30 |
もちろん、面・頂点・辺のうち二つを出し、後は【オイラーの多面体定理】を利用してもOKです。
【オイラーの多面体定理】
頂点の数-辺の数+面の数=2
セリアのTRPG用多面ダイス
なお、このセリアのサイコロ(ダイス)には、【正四面体】【正六面体】【正八面体】【正十二面体】【正二十面体】の五種類に加え、何故か謎の(?)【十面体】が二つも入っています。

もちろん、この【十面体】は【正多面体】ではありません。
僕は最初戸惑ったのですが、そもそもこの商品は、【正多面体】の理解補助のために製作されたものではなく、【テーブルトーク ロールプレイングゲーム(TRPG)】というゲーム(全く知らなかったです。すみません)用に作られたものなんですね。
確かに袋には【TRPG用多面ダイス】と書いてあります。
どこにも「正多面体の理解に最適!」なんて書いてありません(笑)
どうやら
おおっ!
正多面体が100均に!!
と騒いでいるのは、僕たち塾関係者だけ(厳密には、僕の周りの塾関係者だけ)で、世間一般的には
TRPG用ダイスが100均に登場!
的な認識のようです。
算数・数学における語呂合わせ
参考ブログ